By James Leary, Kimberly Burnett and Christopher Wada
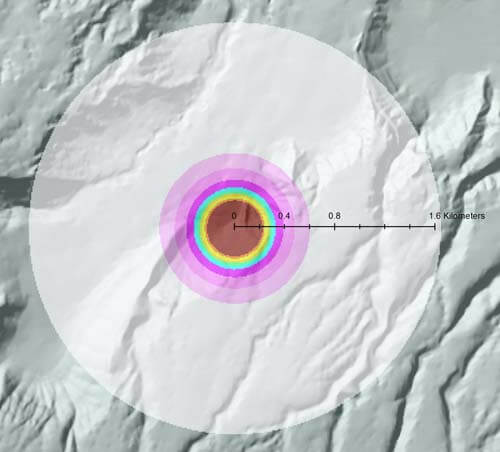
UHERO is working with Dr. James Leary (CTAHR) to assess cost effectiveness of Herbicide Ballistic Technology (HBT) operations to control invasive miconia (Miconia calvescens) plants before reaching maturity. Based on studies in Costa Rica, Tahiti and Australia, we can interpret spatial and temporal implications of management driven by miconia’s fecundity, dispersal, seed bank longevity and recruitment. We find that the dispersal kernel of miconia in the East Maui Watershed is closely matched to a similar probability density function developed from miconia naturalized in North Queensland, Australia (Fletcher and Westcott 2013). In this spatial model, 99% of recruitment was within 609 m with rare stochastic events (i.e., 1%) extending out to 1644 m. Based on these biological features, one autogamous, mature plant can impact up to 850 ha (i.e., 2100 acres) of forested watershed with hundreds to thousands of dispersed progeny germinating asynchronously over several decades (Fig. 1).
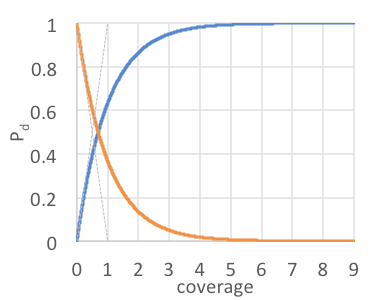
Effective management is achieved when target mortality outpaces biological recruitment. Cacho et al. (2007) coined the term ‘‘mortality factor’’ described by the simple equation: m=Pd x Pk, where the probabilities of detection (Pd ) and kill (Pk)are equal determinants of the “mortality” product. Our current Pk is 0.98 for all HBT treatments. With this effective and reliable treatment technique, management outcomes largely depend on detection (Leary et al. 2013; Lodge et al. 2006). Koopman (1946) introduced the mathematical framework for estimating the probability of detection: Pd=1-e-c, where the probability of detection asymptotically approaches 1.0 with increasing coverage (Fig. 2). In operations, imperfect detection can be compensated by frequent interventions compounding coverage levels over time, but with obvious diminishing returns (Leary et al. 2014).
The variable costs for HBT operations (e.g., flight time and projectiles) are driven by target density (Leary et al 2013, Leary et al. 2014). With that knowledge, we estimate the cost to manage the area (i.e., 850 ha) impacted by the dispersal of new progeny created by a mature plant. A new mature miconia with two panicles may produce ~300-400 progeny. With a single, incipient target being such a high risk, intensive efforts should be matched to comprehensively search the entire impact area over the several decades with a level probability of detection (and equal confirmation of no targets) of all progeny recruits. For instance, with 320 propagules dispersed, Pd would need to exceed 0.9968 with coverage at 5.77 s per 100 m2 pixel totaling ~136 hours of effort over the entire impact area over four decades (Fig. 3A). Any level of coverage less than that (including 99%) would be prone to missing a target that ultimately reaches maturity and newly replenishes the seed bank (Fig. 3B). Furthermore, an overwhelming majority of search effort would actually be dedicated to the confirmation of no targets, where, for instance 87% of effort is invested in looking for 1% of the targets dispersed out to the perimeter.
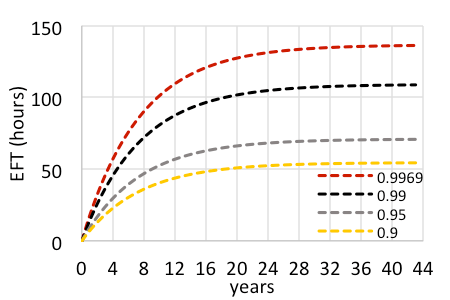
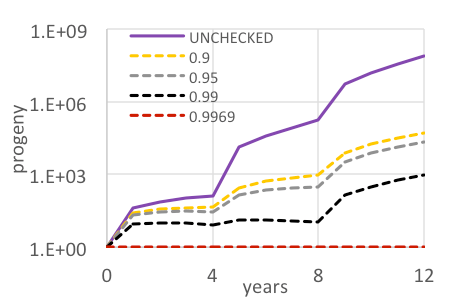
Based on this model, we estimate accrual of future management costs ranging from $169,000-337,000 for every mature target detected, with the increase from the base cost dependent on increasing propagule loads and the static cost to treat each those individuals detected.
BLOG POSTS ARE PRELIMINARY MATERIALS CIRCULATED TO STIMULATE DISCUSSION AND CRITICAL COMMENT. THE VIEWS EXPRESSED ARE THOSE OF THE INDIVIDUAL AUTHORS. WHILE BLOG POSTS BENEFIT FROM ACTIVE UHERO DISCUSSION, THEY HAVE NOT UNDERGONE FORMAL ACADEMIC PEER REVIEW.
References
Cacho, O.J., Hester, S. and Spring, D., 2007. Applying search theory to determine the feasibility of eradicating an invasive population in natural environments. Australian Journal of Agricultural and Resource Economics, 51(4), pp.425-443.
Fletcher C. S. and Westcott D. A.. 2013. Dispersal and the design of effective management strategies for plant invasions: matching scales for success. Ecological Applications 23:1881–1892.
Koopman, B.O. (1946). Search and Screening. Operations Evaluations Group Report no. 56, Center for Naval Analyses, Alexandria, VA.
Leary, J.J., Gooding, J., Chapman, J., Radford, A., Mahnken, B. and Cox, L.J., 2013. Calibration of an Herbicide Ballistic Technology (HBT) helicopter platform targeting Miconia calvescens in Hawaii. Invasive Plant Science and Management, 6(2), pp.292-303.
Leary, J., Mahnken, B.V., Cox, L.J., Radford, A., Yanagida, J., Penniman, T., Duffy, D.C. and Gooding, J., 2014. Reducing nascent miconia (Miconia calvescens) patches with an accelerated intervention strategy utilizing herbicide ballistic technology.
Lodge, D.M., Williams, S., MacIsaac, H.J., Hayes, K.R., Leung, B., Reichard, S., Mack, R.N., Moyle, P.B., Smith, M., Andow, D.A. and Carlton, J.T., 2006. Biological invasions: recommendations for US policy and management. Ecological Applications, 16(6), pp.2035- 2054.